Malaysian Ringgit to US Dollar Exchange Rate Forecast (keras : LSTM) マレーシアリンギットと米ドル為替相場予測

It is so trouble and annoying if currency price change high and down. When should we exchange? Everybody would like to know it..Ops. This is small talk. Let’s get down the business. I tried to creat a model to predict the movement of the currency. This is using keras and LSTM model. But as you can see, data is not sufficient and very simple program. I can not assure how forecast accuracy. Before program, we need to get currency data. I live in Malaysia. I googled and searching data on website. I found only one page below. There seems some specialty companys has long term currency data. But need to pay money. This is just sample.

Regarding Malaysian Ringgit and US Dollar data, You can get below website.

https://markets.businessinsider.com/currencies/usd-myr

Move down the screen and then set the duration of the data you want to get. You can get csv file after click download button.

Notes : It seems the term you can adjust is for nearly 5 years. Even you can set more long term, csv file was downloaded is only nearly 5 years.

The data is included some unnecessary data. Please organize the data.

I use Google Colab. Set the file name as ‘Malaysian Ringgit.csv’, Please load the file according to the environment in which it is being used. The code is as follows.

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, LSTM
from keras import metrics
from sklearn.preprocessing import MinMaxScaler

# Reading data from csv file
df = pd.read_csv('Malaysian Ringgit.csv')
L = len(df)
Hi = np.array([df.iloc[:, 2]]) # Hightest price of day
Low = np.array([df.iloc[:, 3]]) # Lowest price of day
Close = np.array([df.iloc[:, 4]]) # Closing price

# Converting to matrix
Hi = Hi.reshape(-1, 1)
Low = Low.reshape(-1, 1)
Close = Close.reshape(-1, 1)

# Get the data for each of the three days prior
Hi1 = Hi[0:L-3, :]
Low1 = Low[0:L-3, :]
Close1 = Close[0:L-3, :]
Hi2 = Hi[1:L-2, :]
Low2 = Low[1:L-2, :]
Close2 = Close[1:L-2, :]
Hi3 = Hi[2:L-1, :]
Low3 = Low[2:L-1, :]
Close3 = Close[2:L-1, :]

# Combine in 1 dimension
X = np.concatenate([Low1, Hi1, Close1, Low2, Hi2, Close2, Low3, Hi3, Close3], axis=1)
Y = Close[3:L, :]

# Normalize by MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X)
X = scaler.transform(X)

# Normalize by MinMaxScaler
scaler1 = MinMaxScaler()
scaler1.fit(Y)
Y = scaler1.transform(Y)

X = np.reshape(X, (X.shape[0], 1, X.shape[1]))

X_train = X[:190, :, :]
X_test = X[190:, :, :]
Y_train = Y[:190, :]
Y_test = Y[190:, :]

# Create LSTM model
model = Sequential()
model.add(LSTM(100, activation='tanh', input_shape=(1, 9), recurrent_activation='hard_sigmoid'))
model.add(Dense(1))

model.summary()

model.compile(loss='mean_squared_error', optimizer='rmsprop', metrics=[metrics.mae])
model.fit(X_train, Y_train, epochs=100, batch_size=1, verbose=2)

# Predict the output of the model
Predict = model.predict(X_test, verbose=1)

# Undoing normalized data using inverse_transform
Y_train = scaler1.inverse_transform(Y_train)
# Generate a dataframe
Y_train = pd.DataFrame(Y_train)
# Converting a string to a Timestamp type
Y_train.index = pd.to_datetime(df.iloc[3:193,0])

Y_test = scaler1.inverse_transform(Y_test)
Y_test = pd.DataFrame(Y_test)
Y_test.index = pd.to_datetime(df.iloc[193:,0])

Predict = scaler1.inverse_transform(Predict)
Predict = pd.DataFrame(Predict)
Predict.index=pd.to_datetime(df.iloc[193:,0])

# Outputting graph
plt.figure(figsize=(15,10))
plt.plot(Y_test, label = 'Test')
plt.plot(Predict, label = 'Prediction')
plt.legend(loc='best')
plt.show()

The results are as follows

Model: "sequential_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm_3 (LSTM)                (None, 100)               44000     
_________________________________________________________________
dense_3 (Dense)              (None, 1)                 101       
=================================================================
Total params: 44,101
Trainable params: 44,101
Non-trainable params: 0
_________________________________________________________________
Epoch 1/100
 - 1s - loss: 0.0327 - mean_absolute_error: 0.1392
Epoch 2/100
 - 0s - loss: 0.0023 - mean_absolute_error: 0.0359
Epoch 3/100
 - 0s - loss: 0.0025 - mean_absolute_error: 0.0369
Epoch 4/100
 - 0s - loss: 0.0023 - mean_absolute_error: 0.0370
Epoch 5/100
 - 0s - loss: 0.0023 - mean_absolute_error: 0.0358
Epoch 6/100
 - 0s - loss: 0.0022 - mean_absolute_error: 0.0350
Epoch 7/100
 - 0s - loss: 0.0021 - mean_absolute_error: 0.0349
Epoch 8/100
 - 0s - loss: 0.0021 - mean_absolute_error: 0.0343
Epoch 9/100
 - 0s - loss: 0.0020 - mean_absolute_error: 0.0348
Epoch 10/100
 - 0s - loss: 0.0020 - mean_absolute_error: 0.0329
Epoch 11/100
 - 0s - loss: 0.0020 - mean_absolute_error: 0.0322
Epoch 12/100
 - 0s - loss: 0.0019 - mean_absolute_error: 0.0330
Epoch 13/100
 - 0s - loss: 0.0018 - mean_absolute_error: 0.0320
Epoch 14/100
 - 0s - loss: 0.0018 - mean_absolute_error: 0.0313
Epoch 15/100
 - 0s - loss: 0.0018 - mean_absolute_error: 0.0308
Epoch 16/100
 - 0s - loss: 0.0020 - mean_absolute_error: 0.0327
Epoch 17/100
 - 0s - loss: 0.0019 - mean_absolute_error: 0.0327
Epoch 18/100
 - 0s - loss: 0.0019 - mean_absolute_error: 0.0322
Epoch 19/100
 - 0s - loss: 0.0018 - mean_absolute_error: 0.0320
Epoch 20/100
 - 0s - loss: 0.0019 - mean_absolute_error: 0.0313
Epoch 21/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0312
Epoch 22/100
 - 0s - loss: 0.0018 - mean_absolute_error: 0.0308
Epoch 23/100
 - 0s - loss: 0.0017 - mean_absolute_error: 0.0307
Epoch 24/100
 - 0s - loss: 0.0018 - mean_absolute_error: 0.0304
Epoch 25/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0294
Epoch 26/100
 - 0s - loss: 0.0017 - mean_absolute_error: 0.0296
Epoch 27/100
 - 0s - loss: 0.0017 - mean_absolute_error: 0.0305
Epoch 28/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0299
Epoch 29/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0300
Epoch 30/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0309
Epoch 31/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0292
Epoch 32/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0294
Epoch 33/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0298
Epoch 34/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0304
Epoch 35/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0294
Epoch 36/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0299
Epoch 37/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0283
Epoch 38/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0287
Epoch 39/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0282
Epoch 40/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0297
Epoch 41/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0288
Epoch 42/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0294
Epoch 43/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0277
Epoch 44/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0292
Epoch 45/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0272
Epoch 46/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0285
Epoch 47/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0300
Epoch 48/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0273
Epoch 49/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0293
Epoch 50/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0291
Epoch 51/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0283
Epoch 52/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0286
Epoch 53/100
 - 0s - loss: 0.0016 - mean_absolute_error: 0.0287
Epoch 54/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0279
Epoch 55/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0288
Epoch 56/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0281
Epoch 57/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0271
Epoch 58/100
 - 0s - loss: 0.0015 - mean_absolute_error: 0.0294
Epoch 59/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0285
Epoch 60/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0280
Epoch 61/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0280
Epoch 62/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0273
Epoch 63/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0277
Epoch 64/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0273
Epoch 65/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0273
Epoch 66/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0278
Epoch 67/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0272
Epoch 68/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0270
Epoch 69/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0274
Epoch 70/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0279
Epoch 71/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0280
Epoch 72/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0280
Epoch 73/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0274
Epoch 74/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0274
Epoch 75/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0277
Epoch 76/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0271
Epoch 77/100
 - 0s - loss: 0.0012 - mean_absolute_error: 0.0256
Epoch 78/100
 - 0s - loss: 0.0012 - mean_absolute_error: 0.0262
Epoch 79/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0270
Epoch 80/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0269
Epoch 81/100
 - 0s - loss: 0.0012 - mean_absolute_error: 0.0255
Epoch 82/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0267
Epoch 83/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0281
Epoch 84/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0275
Epoch 85/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0270
Epoch 86/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0270
Epoch 87/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0278
Epoch 88/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0268
Epoch 89/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0270
Epoch 90/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0274
Epoch 91/100
 - 0s - loss: 0.0012 - mean_absolute_error: 0.0265
Epoch 92/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0268
Epoch 93/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0273
Epoch 94/100
 - 0s - loss: 0.0014 - mean_absolute_error: 0.0281
Epoch 95/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0273
Epoch 96/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0269
Epoch 97/100
 - 0s - loss: 0.0011 - mean_absolute_error: 0.0261
Epoch 98/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0267
Epoch 99/100
 - 0s - loss: 0.0013 - mean_absolute_error: 0.0272
Epoch 100/100
 - 0s - loss: 0.0012 - mean_absolute_error: 0.0264
1629/1629 [==============================] - 0s 51us/step

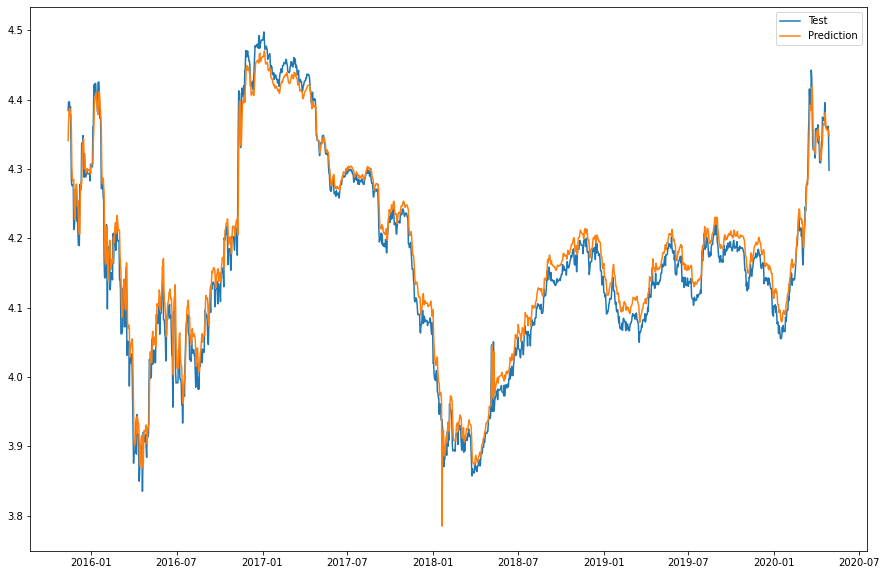
Looking at the graphs, it looks like they’re following and catch-up rather than predicting. No choice. Let’s calculate the percentage of correct answers.

# Simple forecast for the next business day (just rise or fall)
preds = model.predict(X_test)
correct = 0
semi_correct = 0

for i in range(len(preds)):
  pred = np.argmax(preds[i,:])
  tar = np.argmax(X_test[i,:])
  if pred == tar :
    correct += 1

print("Percentage of correct answers to rise and fall:", 1.0 * correct / len(preds))

Percentage of correct answers to rise and fall: 0.4039287906691222

It’s a simple model, but it seems to have a 40% correct answer rate. I will try to enter real number for forecasting next business day’s closing price. Input the price of the high, bottom, and close of the last three days in Excel, and output it to CSV. File name is set as ‘Malaysian Ringgit_price_last_3days.csv’.

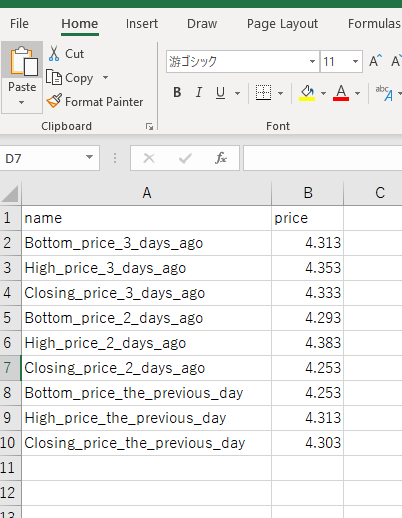
# Read data from csv
forecast_df = pd.read_csv('Malaysian Ringgit_price_last_3days.csv')
forecast_df

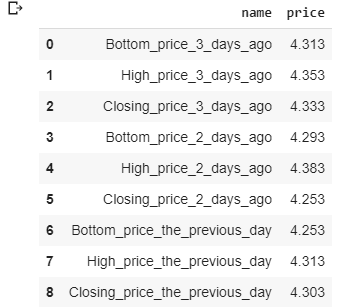
So, let’s read the price column and use predict() to predict a specific future price.

Xnew = np.array([[expect_df['price']]])
Ynew = model.predict(Xnew)
print("入力数値 Entered values=%s\n翌日の予測為替価格 Forecast of the next day's closing price=%s" % (Xnew[0], Ynew[0]))

入力数値 Entered values=[[4.313 4.353 4.333 4.293 4.383 4.253 4.253 4.313 4.303]]
翌日の予測為替価格 Forecast of the next day's closing price=[2.614213]

The average price of the Malaysian ringgit to US dollar exchange over the last three days is 4.3, but the forecast for the next day’s exchange based on that data is 2.6, which is quite different. Changing the model and adding more data may lead to different results. we can’t even take a limit order at a price like this. Haha. There are a lot of web articles on deep learning for stock price prediction, but I didn’t see any articles on specific numerical predictions, so I tried. However, I don’t think we need specific numbers for actual inspections. If we have a high percentage of correct answers that go up or down the next day, it won’t matter. Thank you very much.